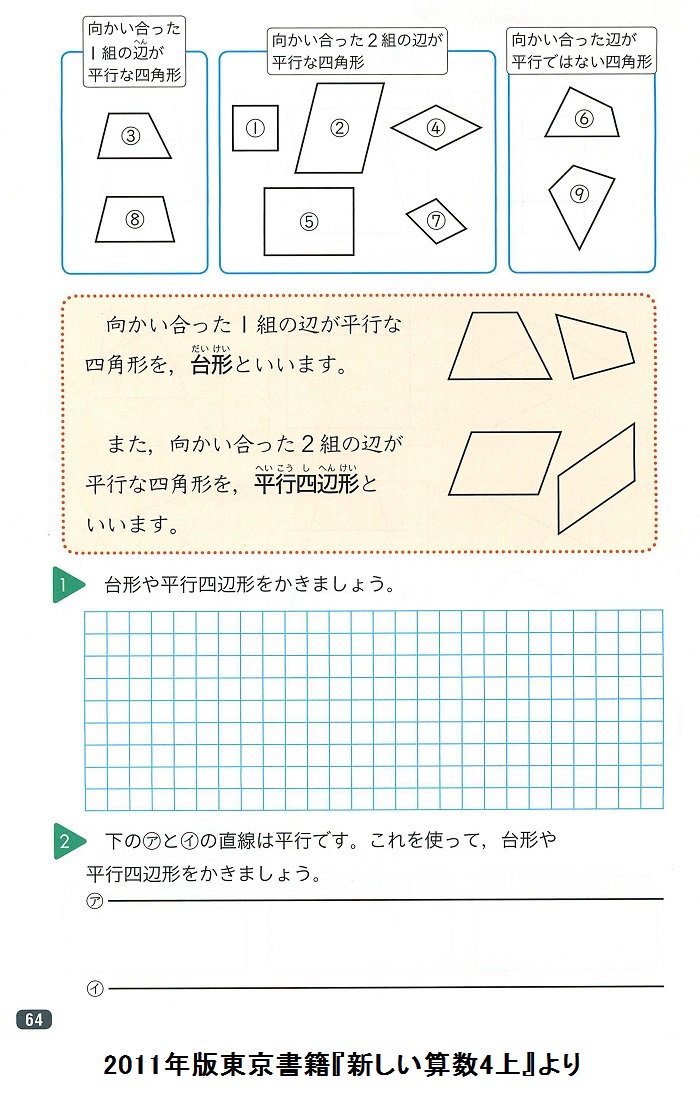
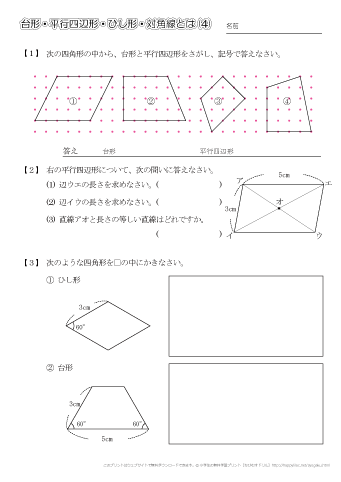
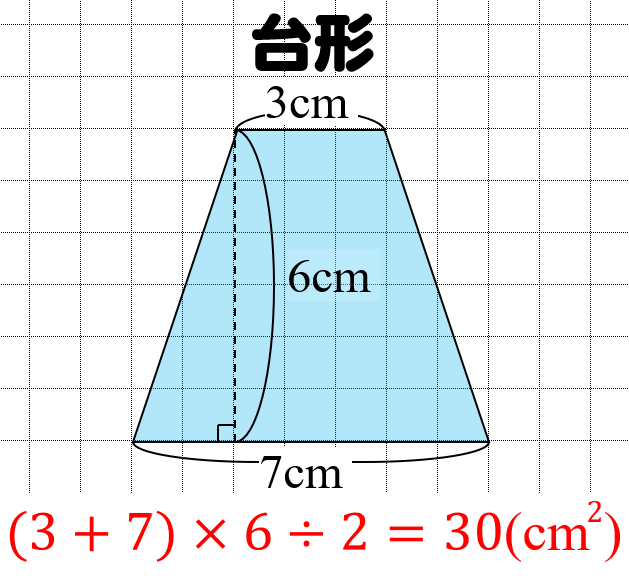
台形とは 算数 165414
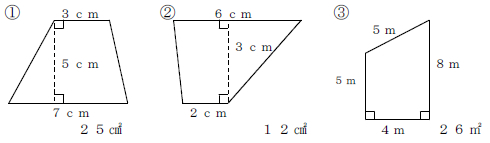
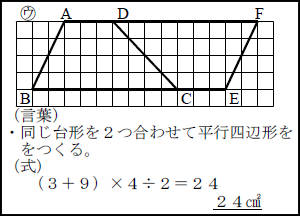
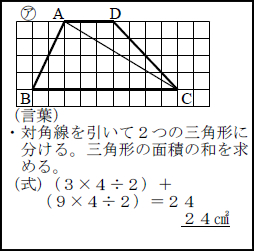
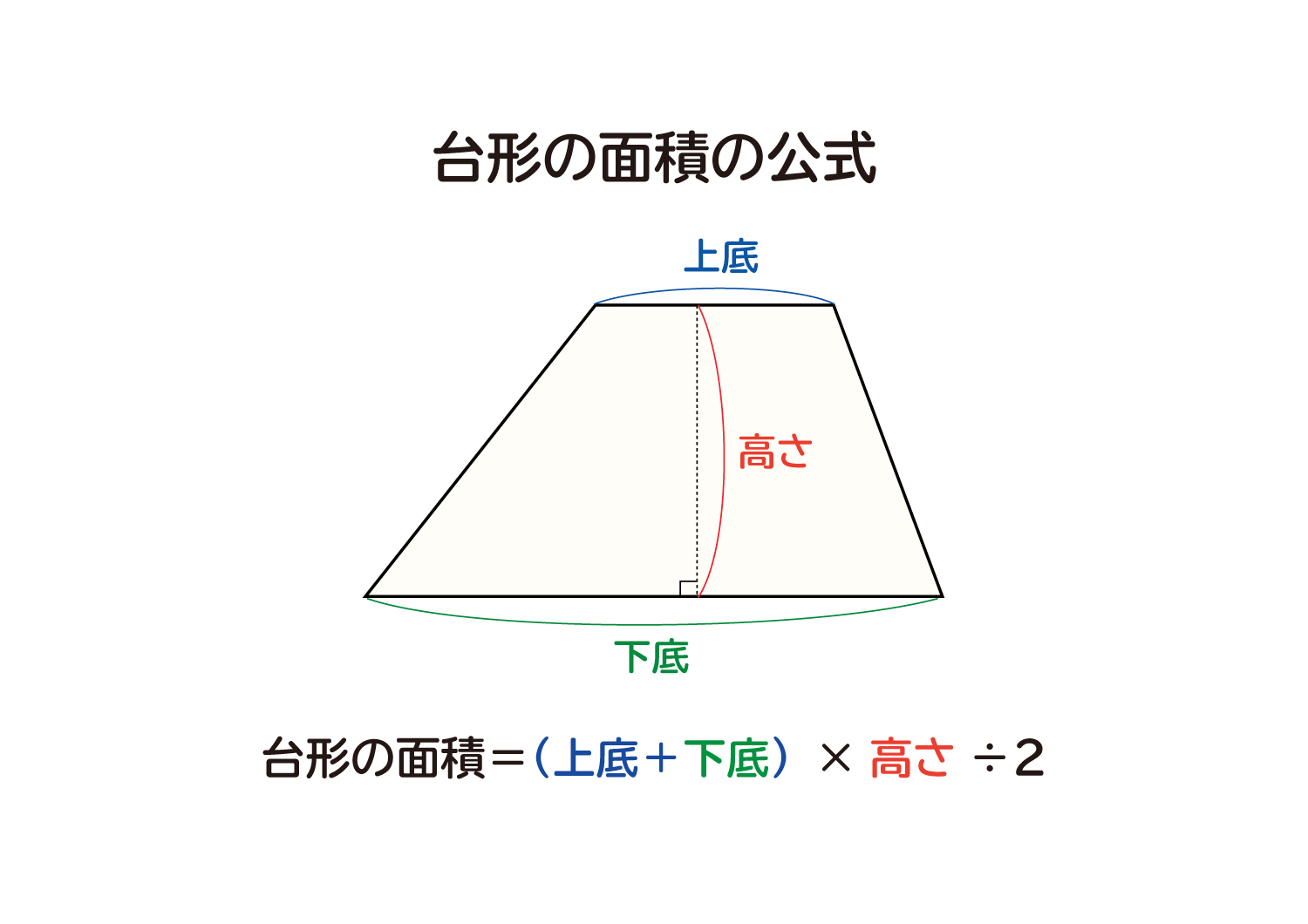
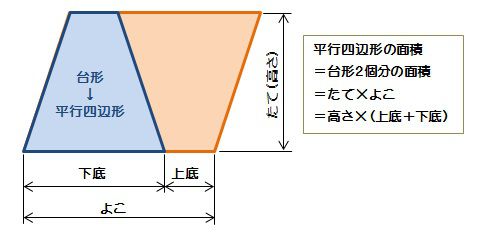
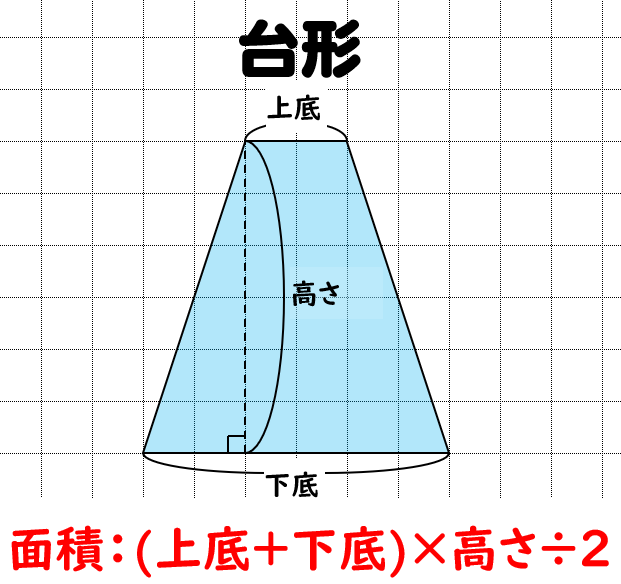
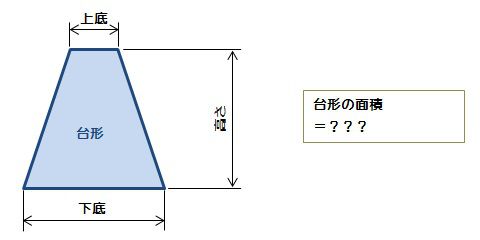
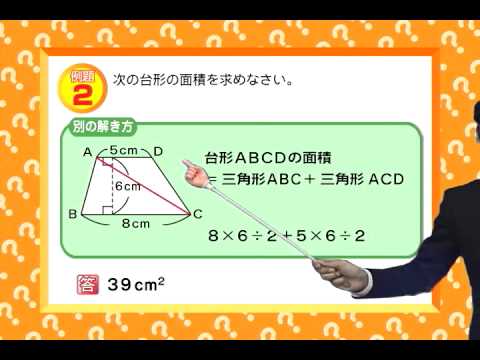
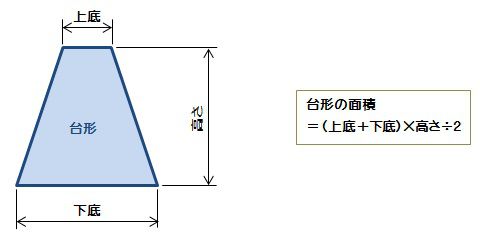
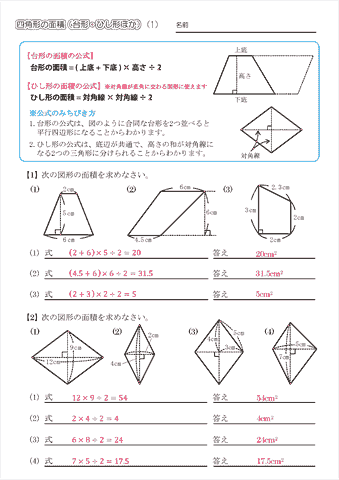
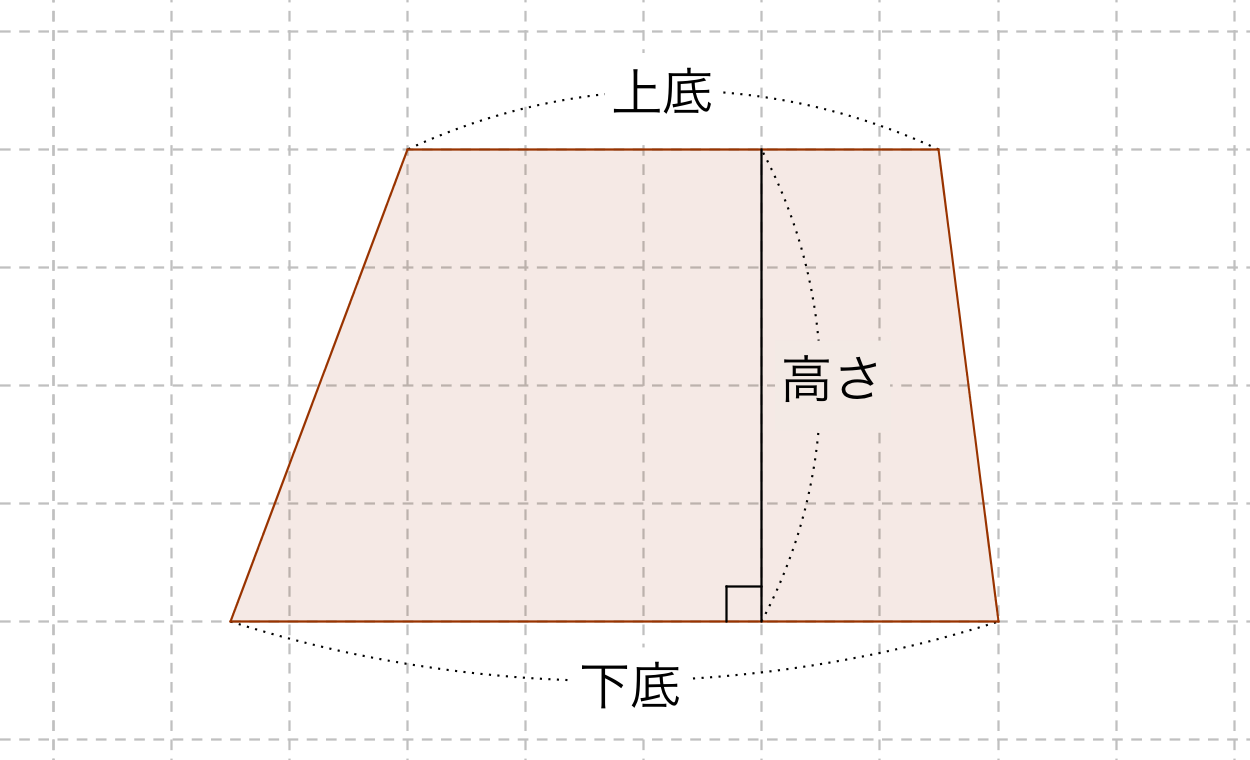
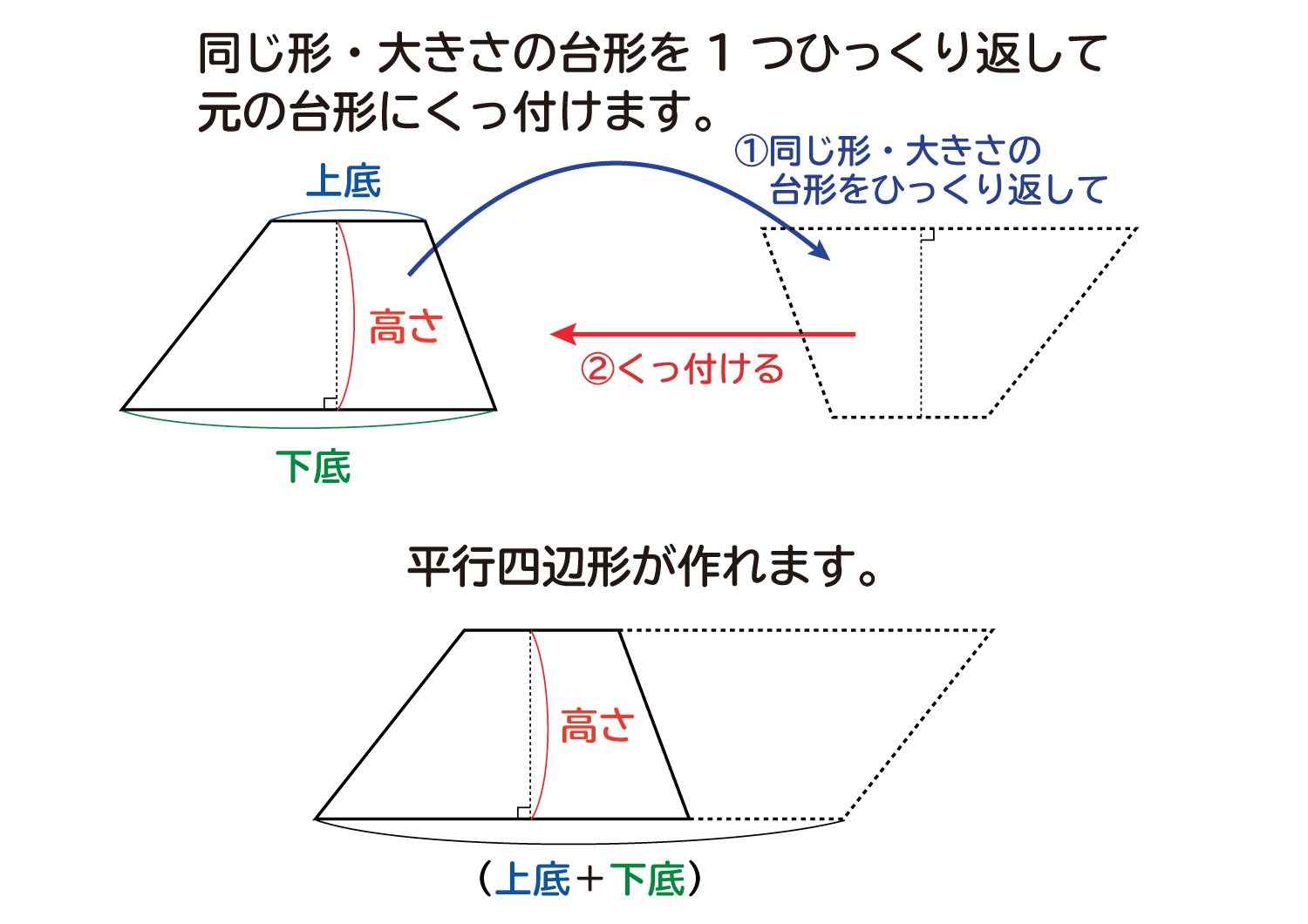
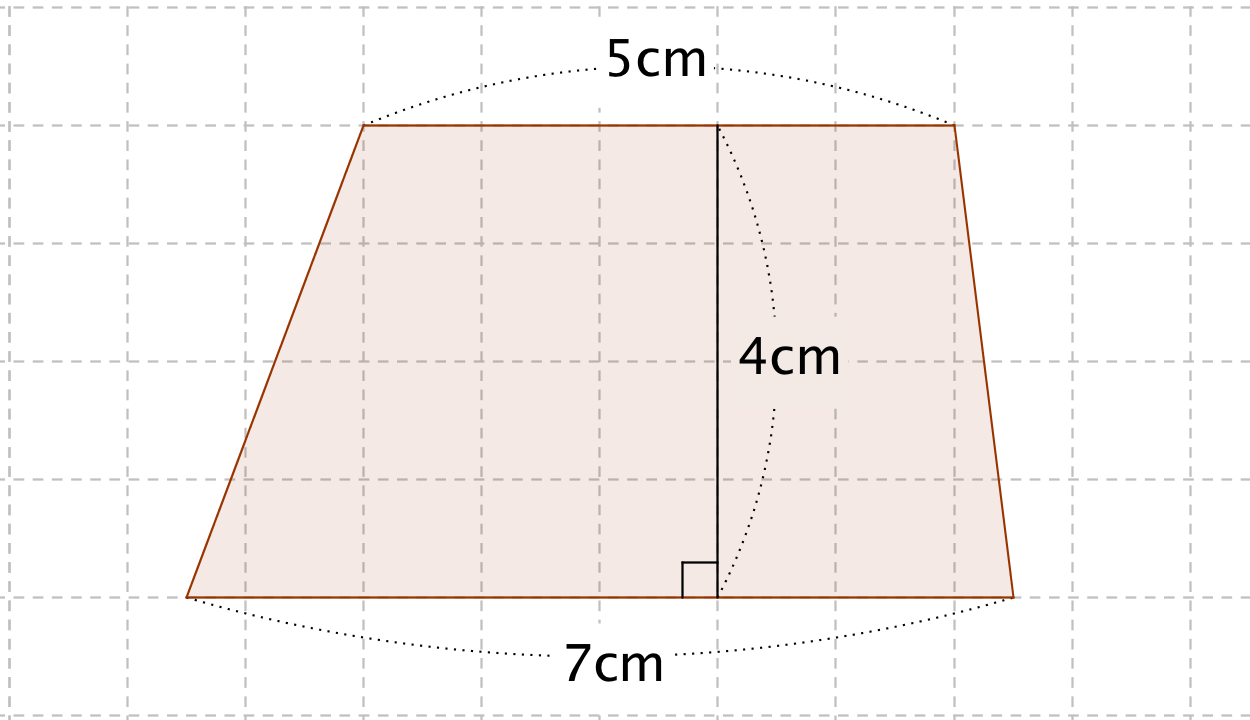
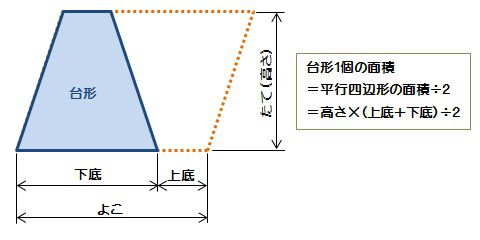
台形の面積は、\(「面積=(上底下底)×高さ÷2」\) で求められます。 たとえば、「上底 \(2cm\),下底 \(6cm\),高さ \(3cm\) の台形」の面積は \((26)×3÷2=12cm^2\) となります。
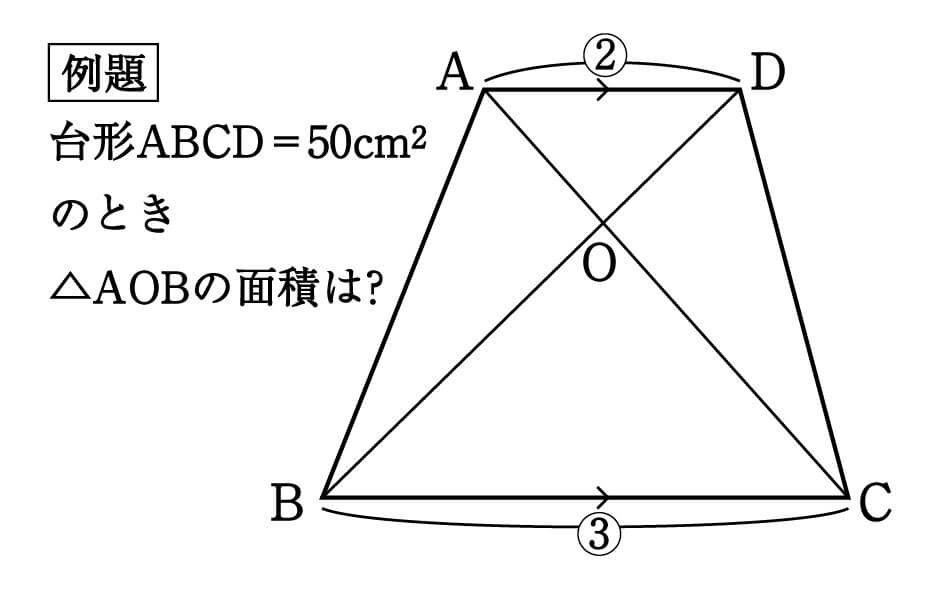
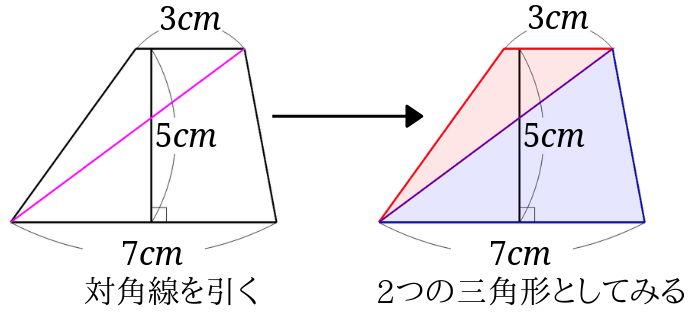
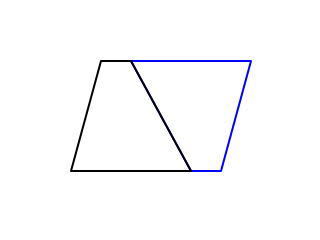
台形とは 算数-相似な図形において、面積比は相似比の2乗になる 比べる図形が相似であれば、相似比を2乗することで面積比を求めることができます。 つまり、台形の中から相似な図形を見つけていくことがポイントになってくるね。 相似な図形において、面積比は相似比の2乗になる 比べる三角形が相似でなくても、高さが等しければ 底辺の長さの比が、そのまま面積比となり台形(赤色) と 台形(青色)は同じ形なので、 \ 台形(赤色)の面積 = 台形(青色)の面積 \ ですね。 よって、(赤色の)台形の面積は \ 台形の面積 = (上底 下底 ) \times 高さ \div 2 \ となります。
台形とは 算数のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  | |
 |  | |
 |  |  |
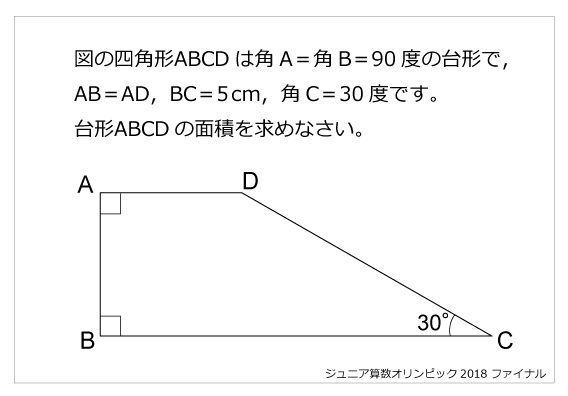
「台形とは 算数」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  |  |
 |  | |
「台形とは 算数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「台形とは 算数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「台形とは 算数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「台形とは 算数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「台形とは 算数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「台形とは 算数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「台形とは 算数」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 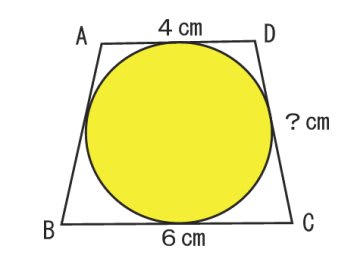 | 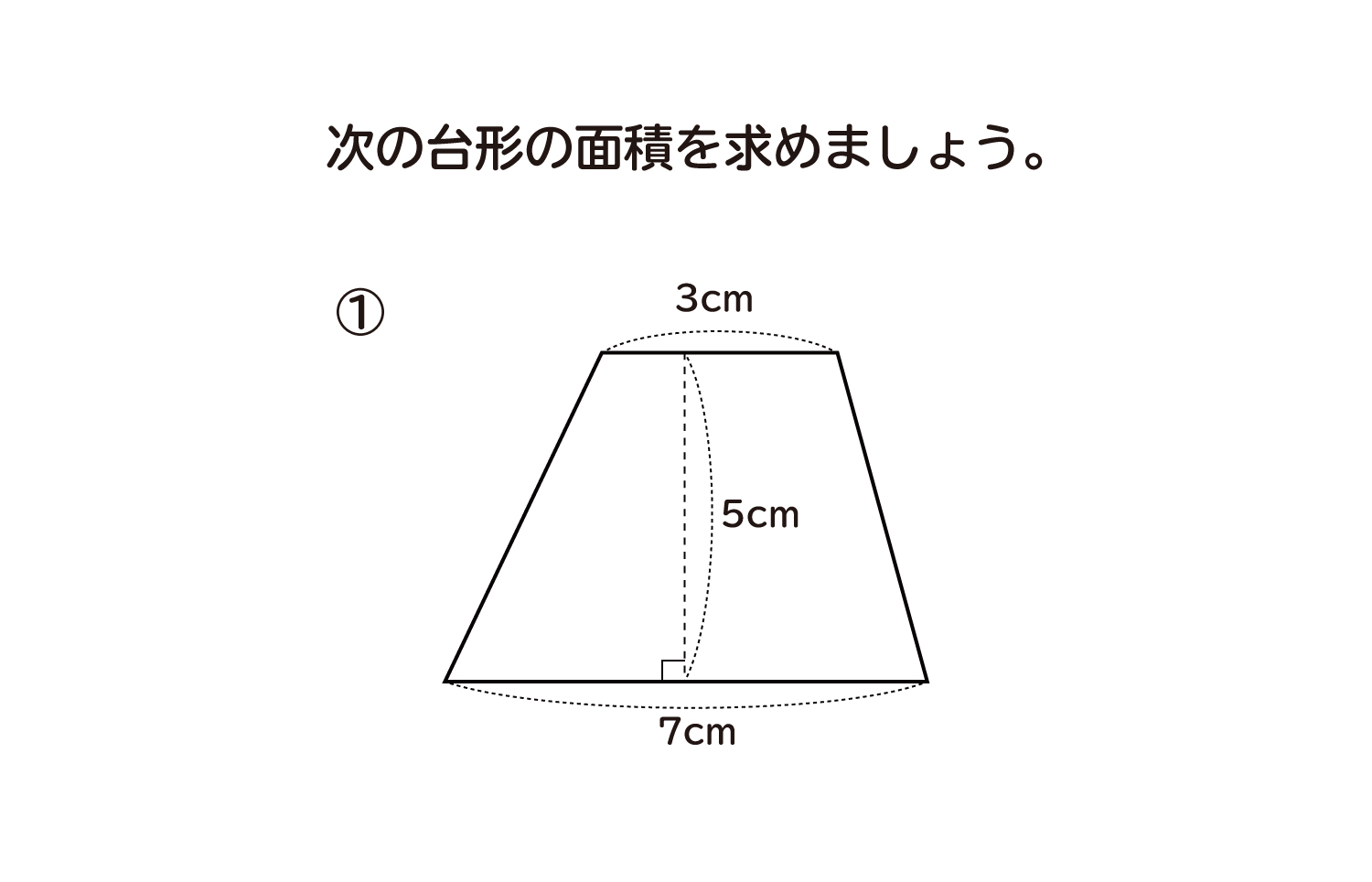 |
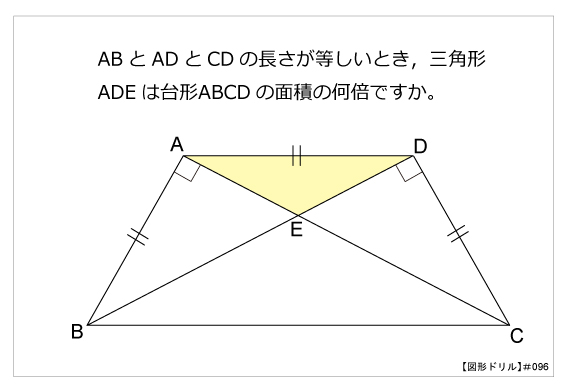 | 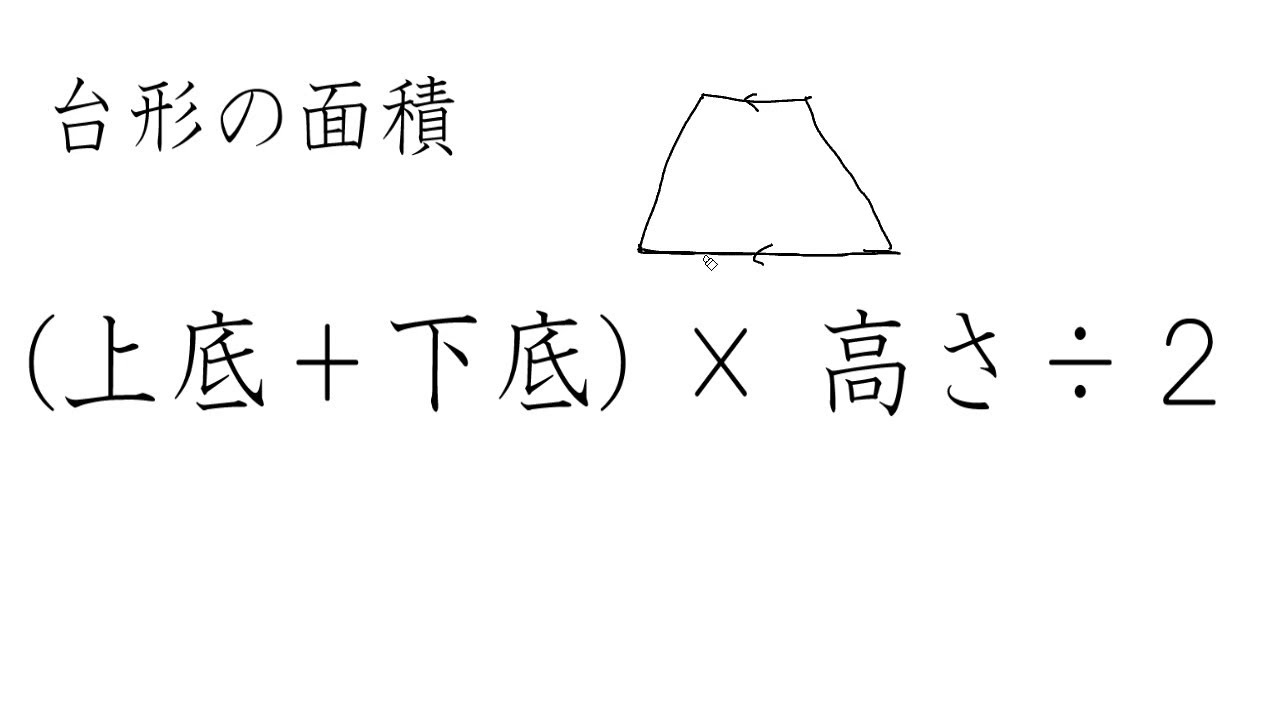 |
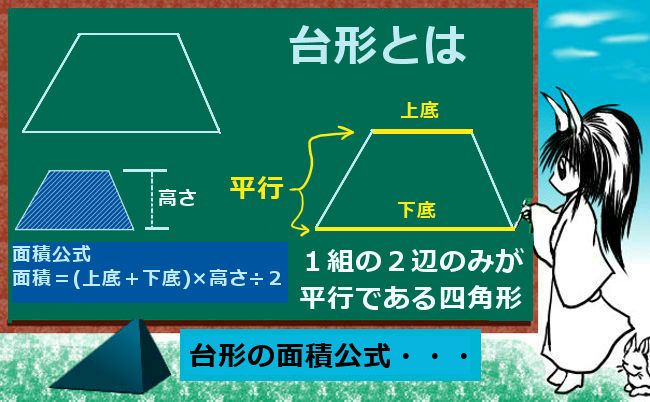
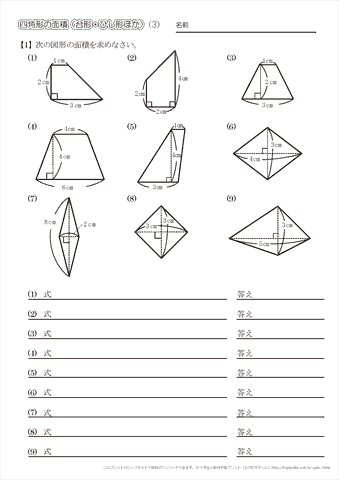
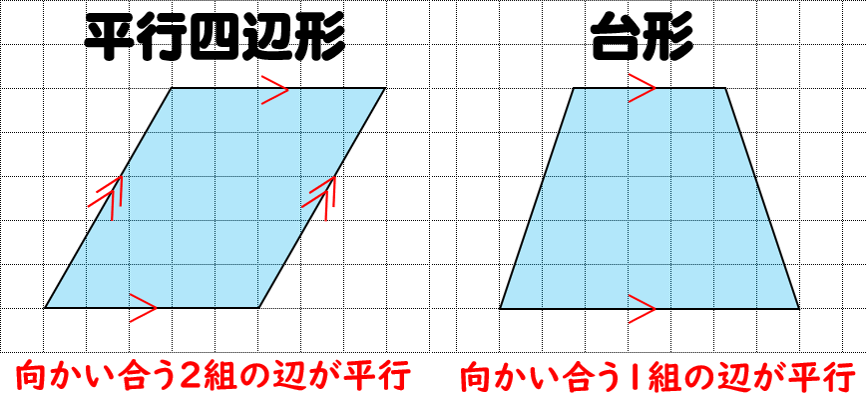
台形の面積を求める公式は、s = {(上底)(下底)}×(高さ)÷2 で表されます。このページでは、台形の面積の求め方を、計算問題と共に説明しています。また、公式の導き方も説明しています。台形 (だいけい、 米 trapezoid 、 英 trapezium )は、 四角形 の一部で、少なくとも一組の対辺が互いに 平行 であるような 図形 である。 平行な2本の対辺を 台形の底辺 といい、そのうち一方を 上底 (じょうてい)、他方を 下底 (かてい)とよぶ。 また、もう一組の対辺を 台形の脚(きゃく) とよぶ。 台形のうち、下底の両端にある2つの 内角 (底角
コメント
コメントを投稿